構造物の振動特性を表す主な要素には、共振周波数（固有振動数）と固有モード、そして「伝達関数」があります。
伝達関数は「構造物に起振力を加えたときの応答」のことで、横軸が周波数、縦軸が加速度（or 速度、変位）を「力」で割った値になります。起振力が大きければ振動も大きくなるため、「単位力分の加速度」とすることで、様々な構造を横並び比較できるようになります。
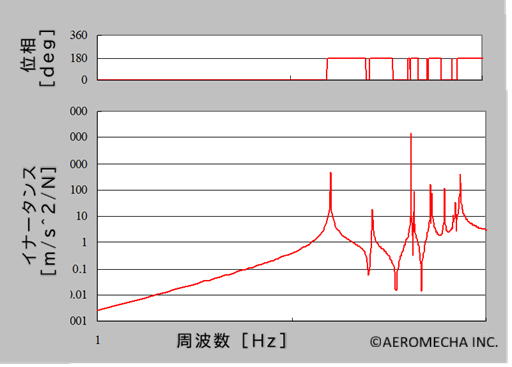
構造物のメッシュモデルを周波数応答解析するとFigure 3.1のような伝達関数が算出されます。
縦軸が「加速度/力」の伝達関数を「イナータンス」といいます。

周波数応答のグラフのことを伝達関数と呼ぶのは、そのグラフが質量、剛性、減衰を変数とする運動方程式=関数により描かれるからです。
質量、剛性、減衰が変われば伝達関数の波形も変化するため、波形を見れば構造の状態をある程度知ることができます。
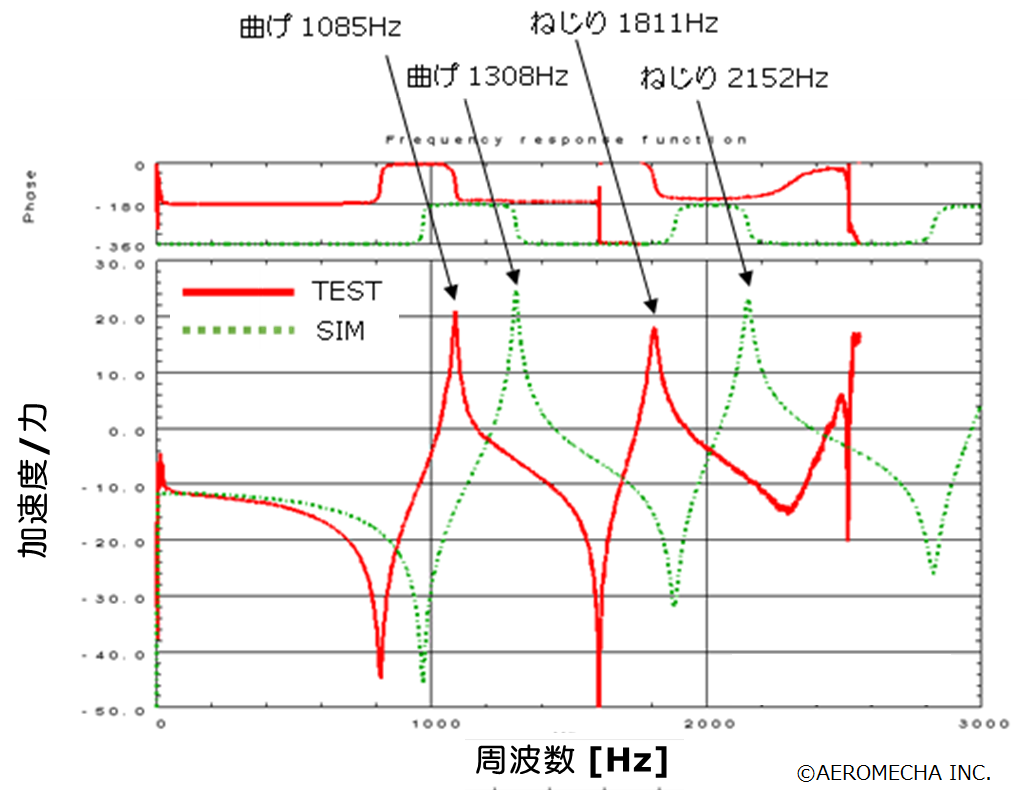
たとえばFigure 3.2は、ある構造物のイナータンスを実測（TEST）と解析※（SIM）で比較したものですが、解析が実測に対し全般的に高周波側へずれていることがわかります。※CAEの世界ではシミュレーション結果を「解析結果」と呼ぶことが多いです。
この結果から、解析に用いたメッシュモデルは共振周波数が高めであるため、モデルの形状（断面）が実機と一致していないことが見えてきます。