2) 重量物のイナーシャ（慣性モーメント）
モータやエンジンその他電源装置のような重量物が搭載される構造物では、それらを単に質点としてモデル化しただけでは伝達関数（周波数応答波形）が実測値を再現しないことがあります。これは全系振動に対し重量物のイナーシャの影響が大きい場合に生じます。全体構造における質量比率が比較的大きいコンポーネントについては、イナーシャ（慣性モーメント）を集中マスに追加定義することで、全系振動が精度よく再現されるようになります。
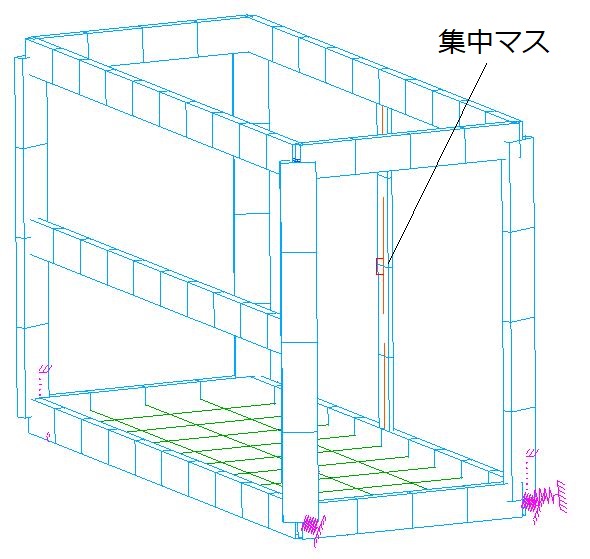
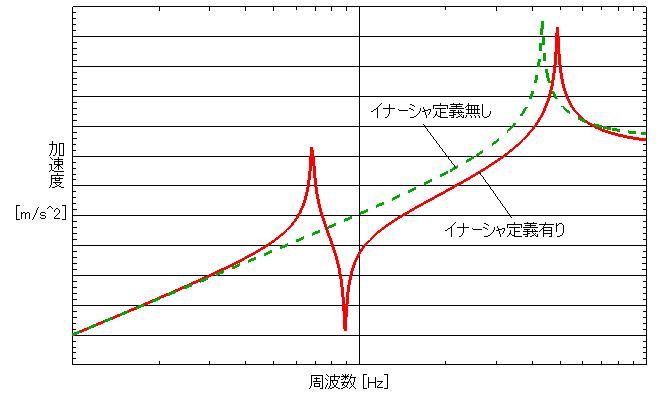
例題構造の集中マスにイナーシャを定義した場合（イナーシャ定義有り）と定義しない場合（イナーシャ定義無し）の場合の伝達関数をFigure 2.2に示します。「イナーシャ定義有り」に現れている低周波側のピークが「イナーシャ定義無し」では現れていません。イナーシャは共振周波数の変化だけでなく、固有モードのh振動形態を変化させることがあります。イナーシャは簡易な形状であれば手計算でも算出できますが、多くの場合、CADデータから算出します。
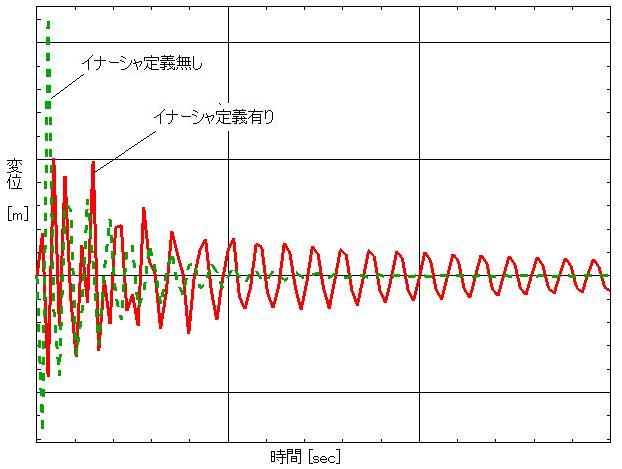
イナーシャは、その値が大きいほど振動しにくく、いったん振動が始まると今度は振動が止まりにくいという特徴があります。たとえば、割りばしの真ん中を糸で釣ったものと、丸太の真ん中をロープで釣ったものを比べます。イナーシャの小さな割りばしは指を触れるだけで回転しますが、イナーシャの大きい丸太は手で押してやらないと回転しません。またその逆に、いったん回転をはじめた丸太を止めるには大きな力を要します。例題構造の集中マスにイナーシャを定義した場合（イナーシャ定義有り）と定義しない場合（イナーシャ定義無し）の時刻歴波形にはその特徴がよく表れています。（Figure 2.3）「イナーシャ定義有り」ではいつまでも振動がゼロに収束しないのに対し、「イナーシャ定義無し」では短時間でゼロレベルまで減衰しています。
.
次ページでは、「3) 固定部の取り付け点剛性（局所剛性）」についてご紹介いたします。
CAE解析サービス
振動試験サービス
